1  From calculator to computer

Let us consider a basic calculator with buttons to add, subtract, multiply, divide, and take square roots. Using such a simple thing is certainly familiar for any reader of these notes. Indeed, a familiarity with a graphing calculator is expected. Julia makes these familiar tasks just as easy, offering numerous conveniences along the way. In this section we describe how.

The following image is the calculator that Google presents upon searching for “calculator.”

Screenshot of a calculator provided by the Google search engine.

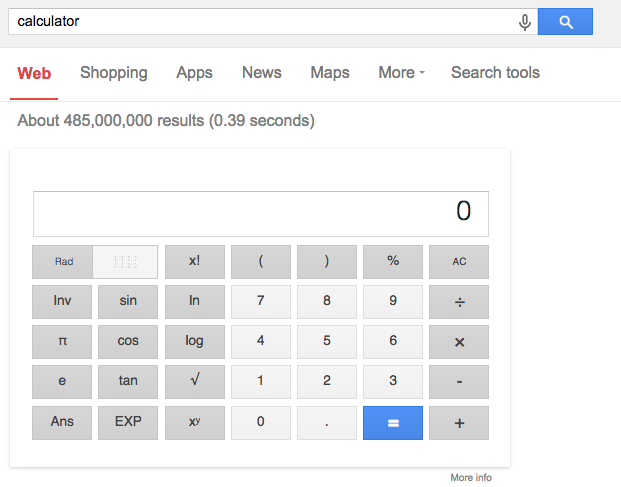
This calculator should have a familiar appearance with a keypad of numbers, a set of buttons for arithmetic operations, a set of buttons for some common mathematical functions, a degree/radian switch, and buttons for interacting with the calculator: Ans, AC (also CE), and =.

The goal here is to see the counterparts within Julia to these features.

---

For an illustration of a really basic calculator, have some fun watching this video:

1.1 Operations

Performing a simple computation on the calculator typically involves hitting buttons in a sequence, such as “1”, “+”, “2”, “=” to compute 3 from adding 1 + 2. In Julia, the process is not so different. Instead of pressing buttons, the various values are typed in. So, we would have:

1 + 2

3

Sending an expression to Julia’s interpreter - the equivalent of pressing the “=” key on a calculator - is done at the command line by pressing the Enter or Return key, and in Pluto, also using the “play” icon, or the keyboard shortcut Shift-Enter. If the current expression is complete, then Julia evaluates it and shows any output. If the expression is not complete, Julia’s response depends on how it is being called. Within Pluto, a message about “premature end of input” is given. If the expression raises an error, this will be noted.

The basic arithmetic operations on a calculator are “+”, “-”, “×”, “÷”, and “\(xʸ\)”. These have parallels in Julia through the binary operators: +, -, *, /, and ^:

1 + 2, 2 - 3, 3 * 4, 4 / 5, 5 ^ 6

(3, -1, 12, 0.8, 15625)

On some calculators, there is a distinction between minus signs - the binary minus sign and the unary minus sign to create values such as \(-1\).

In Julia, the same symbol, “-”, is used for each:

-1 - 2

-3

An expression like \(6 - -3\), subtracting minus three from six, must be handled with some care. With the Google calculator, the expression must be entered with accompanying parentheses: \(6 -(-3)\). In Julia, parentheses may be used, but are not needed. However, if omitted, a space is required between the two minus signs:

6 - -3

9

(If no space is included, the value “--” is parsed like a different, invalid, operation.)

Warning

Julia only uses one symbol for minus, but web pages may not! Copying and pasting an expression with a minus sign can lead to hard to understand errors such as: invalid character "−". There are several Unicode symbols that look similar to the ASCII minus sign, though different. These notes use a different character for the minus sign for the typeset math (e.g., \(1 - \pi\)) than for the code within cells (e.g. 1 - 2). Thus, copying and pasting the typeset math may not work as expected.

1.1.1 Examples

Example

For everyday temperatures, the conversion from Celsius to Fahrenheit (\(9/5 C + 32\)) is well approximated by simply doubling and adding \(30\). Compare these values for an average room temperature, \(C=20\), and for a relatively chilly day, \(C=5\):

For \(C=20\):

9 / 5 * 20 + 32

68.0

The easy to compute approximate value is:

2 * 20 + 30

70

The difference is:

(9/5*20 + 32) - (2 * 20 + 30)

-2.0

For \(C=5\), we have the actual value of:

9 / 5 * 5 + 32

41.0

and the easy to compute value is simply \(40 = 10 + 30\). The difference is

(9 / 5 * 5 + 32) - 40

1.0

Example

Add the numbers \(1 + 2 + 3 + 4 + 5\).

1 + 2 + 3 + 4 + 5

15

Example

How small is \(1/2/3/4/5/6\)? It is about \(14/10,000\), as this will show:

1/2/3/4/5/6

0.001388888888888889

Example

Which is bigger \(4^3\) or \(3^4\)? We can check by computing their difference:

4^3 - 3^4

-17

So \(3^4\) is bigger.

Example

A right triangle has sides \(a=11\) and \(b=12\). Find the length of the hypotenuse squared. As \(c^2 = a^2 + b^2\) we have:

11^2 + 12^2

265

Example

A overview of a research paper published in theconversation.com reviews six authors’ work on estimating the number of ants currently on earth. This was covered in an article in the Washington Post.

The authors describe the number of ants two ways:

• There are \(20 \cdot 10^{15}\) (20 quadrillion or 20 thousand million millions) ants.

• There is an estimated total biomass of \(12\) megatons of dry carbon.

The authors note in a supplement to their paper that over 15,700 species and subspecies of ants have been named. To get a good estimate, 489 studies of ant populations were combined spanning all continents and major habitats. The studies identify the number of foraging ants and combined yield the estimates for the epigaeic ant abundance (\(3.02 \cdot 10^{15}\)) and the arboreal ant abundance (\(1.34\cdot 10^{15}\)). Using an estimate of 22% of ants in a colony are foraging, they get the following estimate for the number of ants:

(3.02 * 10^15 + 1.34*10^15) * 100 / 22

1.981818181818182e16

Shifting the decimal point, this gives a value rounded to \(20\cdot 10^{15}\) ants.

The authors used a value for the dry weight of an average (and representative) single ant. What was that value? (Which they indicate is perhaps unreliable, as, for example, small-bodied ants may be much more abundant than large-bodied ants). We assume below that one “megaton” is \(1\) million metric tons; a metric ton is \(1,000\) kilograms; and a kilogram \(1,000\) grams:

(12 * 1_000_000 * 1_000 * 1_000) / 20_000_000_000_000_000

0.0006

Which translates to an average dry carbon weight of \(0.6/1000\) grams, that is \(0.6\) milligrams (\(0.62\) mg C was actually used).

The authors write that insects are generally considered to have a dry weight of 30% wet weight, and a carbon weight of 50% dry weight, so the weight in grams of an average living ant would be multiplied by \(2\) and then \(10/3\):

(12 * 1_000_000 * 1_000 * 1_000) / 20_000_000_000_000_000 * (2 * 10/3)

0.004

That is 4 milligrams, or 250 ants per gram on average.

Numeric combinations, as above, will be easier to check for correctness when variable names are assigned to the respective values.

Using the underscore, as above, to separate groups of digits, is helpful, as an alternate to scientific notation, when working with large numbers.

1.2 Order of operations

The calculator must use some rules to define how it will evaluate its instructions when two or more operations are involved. We know mathematically, that when \(1 + 2 \cdot 3\) is to be evaluated the multiplication is done first then the addition.

With the Google Calculator, typing 1 + 2 x 3 = will give the value \(7\), but if we evaluate the + sign first, via 1 + 2 = x 3 = the answer will be 9, as that will force the addition of 1+2 before multiplying. The more traditional way of performing that calculation is to use parentheses to force an evaluation. That is, (1 + 2) * 3 = will produce 9 (though one must type it in, and not use a mouse to enter). Except for the most primitive of calculators, there are dedicated buttons for parentheses to group expressions.

In Julia, the entire expression is typed in before being evaluated, so the usual conventions of mathematics related to the order of operations may be used. These are colloquially summarized by the acronym PEMDAS.

PEMDAS. This acronym stands for Parentheses, Exponents, Multiplication, Division, Addition, Subtraction. The order indicates which operation has higher precedence, or should happen first. This isn’t exactly the case, as “M” and “D” have the same precedence, as do “A” and “S”. In the case of two operations with equal precedence, associativity is used to decide which to do. For the operations +, -, *, / the associativity is left to right, as in the left one is done first, then the right. However, ^ has right associativity, so 4^3^2 is 4^(3^2) and not (4^3)^2. (Be warned that some calculators - and spread sheets, such as Excel - will treat this expression with left associativity.)

With rules of precedence, an expression like the following has a clear interpretation to Julia without the need for parentheses:

1 + 2 - 3 * 4 / 5 ^ 6

2.999232

Working through PEMDAS we see that ^ is first, then * and then / (this due to associativity and * being the leftmost expression of the two) and finally + and then -, again by associativity rules. So we should have the same value with:

(1 + 2) - ((3 * 4) / (5 ^ 6))

2.999232

If different parentheses are used, the answer will likely be different. For example, the following forces the operations to be -, then *, then +. The result of that is then divided by 5^6:

(1 + ((2 - 3) * 4)) / (5 ^ 6)

-0.000192

1.2.1 Examples

Example

The percentage error in \(x\) if \(y\) is the correct value is \((x-y)/y \cdot 100\). Compute this if \(x=100\) and \(y=98.6\).

(100 - 98.6) / 98.6 * 100

1.4198782961460505

Example

The marginal cost of producing one unit can be computed by finding the cost for \(n+1\) units and subtracting the cost for \(n\) units. If the cost of \(n\) units is \(n^2 + 10\), find the marginal cost when \(n=100\).

(101^2 + 10) - (100^2 + 10)

201

Example

The average cost per unit is the total cost divided by the number of units. Again, if the cost of \(n\) units is \(n^2 + 10\), find the average cost for \(n=100\) units.

(100^2 + 10) / 100

100.1

Example

The slope of the line through two points is \(m=(y_1 - y_0) / (x_1 - x_0)\). For the two points \((1,2)\) and \((3,4)\) find the slope of the line through them.

(4 - 2) / (3 - 1)

1.0

1.2.2 Two ways to write division - and they are not the same

The expression \(a + b / c + d\) is equivalent to \(a + (b/c) + d\) due to the order of operations. It will generally have a different answer than \((a + b) / (c + d)\).

How would the following be expressed, were it written inline:

\[ \frac{1 + 2}{3 + 4}? \]

It would have to be computed through \((1 + 2) / (3 + 4)\). This is because unlike /, the implied order of operation in the mathematical notation with the horizontal division symbol (the vincula) is to compute the top and the bottom and then divide. That is, the vincula is a grouping notation like parentheses, only implicitly so. Thus the above expression really represents the more verbose:

\[ \frac{(1 + 2)}{(3 + 4)}. \]

Which lends itself readily to the translation:

(1 + 2) / (3 + 4)

0.42857142857142855

To emphasize, this is not the same as the value without the parentheses:

1 + 2 / 3 + 4

5.666666666666666

Warning

The vinculum also indicates grouping when used with the square root (the top bar), and complex conjugation. That usage is often clear enough, but the usage of the vinculum in division often leads to confusion. The example above is one where the parentheses are often, erroneously, omitted. However, more confusion can arise when there is more than one vincula. An expression such as \(a/b/c\) written inline has no confusion, it is: \((a/b) / c\) as left association is used; but when written with a pair of vincula there is often the typographical convention of a slightly longer vincula to indicate which is to be considered first. In the absence of that, then top to bottom association is often implied.

1.2.3 Infix, postfix, and prefix notation

The factorial button on the Google Button creates an expression like 14! that is then evaluated. The operator, !, appears after the value (14) that it is applied to. This is called postfix notation. When a unary minus sign is used, as in -14, the minus sign occurs before the value it operates on. This uses prefix notation. These concepts can be extended to binary operations, where a third possibility is provided: infix notation, where the operator is between the two values. The infix notation is common for our familiar mathematical operations. We write 14 + 2 and not + 14 2 or 14 2 +. (Though if we had an old reverse-Polish notation calculator, we would enter 14 2 +!) In Julia, there are several infix operators, such as +, -, … and others that we may be unfamiliar with. These mirror the familiar notation from most math texts.

Note

In Julia many infix operations can be done using a prefix manner. For example 14 + 2 can also be evaluated by +(14,2). There are very few postfix operations, though in these notes we will overload one, the ' operation, to indicate a derivative.

1.3 Constants

The Google calculator has two built in constants, e and π. Julia provides these as well, though not quite as easily. First, π is just pi:

pi

π = 3.1415926535897...

Whereas, e is is not simply the character e, but rather a Unicode character typed in as \euler[tab].

ℯ

ℯ = 2.7182818284590...

Note

However, when the accompanying package, CalculusWithJulia, is loaded, the character e will refer to a floating point approximation to the Euler constant .

In the sequel, we will just use e for this constant (though more commonly the exp function), with the reminder that base Julia alone does not reserve this symbol.

Mathematically these are irrational values with decimal expansions that do not repeat. Julia represents these values internally with additional accuracy beyond that which is displayed. Math constants can be used as though they were numbers, such is done with this expression:

ℯ^(1/(2*pi))

1.17251960642002

Warning

In most cases. There are occasional (basically rare) spots where using pi by itself causes an error where 1*pi will not. The reason is 1*pi will create a floating point value from the irrational object, pi.

1.3.1 Numeric literals

For some special cases, Julia parses multiplication without a multiplication symbol. This is when the value on the left is a number, as in 2pi, which has an equivalent value to 2*pi. However the two are not equivalent, in that multiplication with numeric literals does not have the same precedence as regular multiplication - it is higher. This has practical importance when used in division or powers. For instance, these two are not the same:

1/2pi, 1/2*pi

(0.15915494309189535, 1.5707963267948966)

Why? Because the first 2pi is performed before division, as multiplication with numeric literals has higher precedence than regular multiplication, which is at the same level as division.

To confuse things even more, consider

2pi^2pi

2658.978166443007

Is this the same as 2 * (pi^2) * pi or (2pi)^(2pi)? The former would be the case is powers had higher precedence than literal multiplication, the latter would be the case were it the reverse. In fact, the correct answer is 2 * (pi^(2*pi)):

2pi^2pi, 2 * (pi/2) * pi, (2pi)^(2pi), 2 * (pi^(2pi))

(2658.978166443007, 9.869604401089358, 103540.92043427199, 2658.978166443007)

This follows usual mathematical convention, but is a source of potential confusion. It can be best to be explicit about multiplication, save for the simplest of cases.

1.4 Functions

On the Google calculator, the square root button has a single purpose: for the current value find a square root if possible, and if not signal an error (such as what happens if the value is negative). For more general powers, the \(x^y\) key can be used.

In Julia, functions are used to perform the actions that a specialized button may do on the calculator. Julia provides many standard mathematical functions - more than there could be buttons on a calculator - and allows the user to easily define their own functions. For example, Julia provides the same set of functions as on Google’s calculator, though with different names. For logarithms, \(\ln\) becomes log and \(\log\) is log10 (computer programs almost exclusively reserve log for the natural log); for factorials, \(x!\), there is factorial; for powers \(\sqrt{...}\) becomes sqrt, \(EXP\) becomes exp, and \(x^y\) is computed with the infix operator ^. For the trigonometric functions, the basic names are similar: sin, cos, tan. These expect radians. For angles in degrees, the convenience functions sind, cosd, and tand are provided. On the calculator, inverse functions like \(\sin^{-1}(x)\) are done by combining \(Inv\) with \(\sin\). With Julia, the function name is asin, an abbreviation for “arcsine.” (Which is a good thing, as the notation using a power of \(-1\) is often a source of confusion and is not supported by Julia without work.) Similarly, there are asind, acos, acosd, atan, and atand functions available to the Julia user.

The following table summarizes the above:

Calculator	Julia
\(+\), \(-\), \(\times\), \(\div\)	+, -, *, /
\(x^y\)	^
\(\sqrt{...}, \sqrt[3]{...}\)	sqrt, cbrt
\(e^x\)	exp
\(\ln\), \(\log\)	log, log10
\(\sin, \cos, \tan, \sec, \csc, \cot\)	sin, cos, tan, sec, csc, cot
In degrees, not radians	sind, cosd, tand, secd, cscd, cotd
\(\sin^{-1}, \cos^{-1}, \tan^{-1}\)	asin, acos, atan
\(n!\)	factorial

Using a function is very straightforward. A function is called using parentheses, in a manner visually similar to how a function is called mathematically. So if we consider the sqrt function, we have:

sqrt(4), sqrt(5)

(2.0, 2.23606797749979)

The function is referred to by name (sqrt) and called with parentheses. Any arguments are passed into the function using commas to separate values, should there be more than one. When there are numerous values for a function, the arguments may need to be given in a specific order or may possibly be specified with keywords. (A semicolon can be used instead of a comma to separate keyword arguments.)

Some more examples:

exp(2), log(10), sqrt(100), 10^(1/2)

(7.38905609893065, 2.302585092994046, 10.0, 3.1622776601683795)

Note

Parentheses have many roles. We’ve just seen that parentheses may be used for grouping, and now we see they are used to indicate a function is being called. These are familiar from their parallel usage in traditional math notation. In Julia, a third usage is common, the making of a “tuple,” or a container of different objects, for example (1, sqrt(2), pi). In these notes, the output of multiple commands separated by commas is a printed tuple.

1.4.1 Multiple arguments

For the logarithm, we mentioned that log is the natural log and log10 implements the logarithm base 10. As well there is log2. However, in general there is no logb for any base b. Instead, the basic log function can take two arguments. When it does, the first is the base, and the second the value to take the logarithm of. This avoids forcing the user to remember that \(\log_b(x) = \log(x)/\log(b)\).

So we have all these different, but related, uses to find logarithms:

log(e), log(2, e), log(10, e), log(e, 2)

(1.0, 1.4426950408889634, 0.43429448190325176, 0.6931471805599453)

In Julia, the “generic” function log not only has different implementations for different types of arguments (real or complex), but also has a different implementation depending on the number of arguments.

1.4.2 Examples

Example

A right triangle has sides \(a=11\) and \(b=12\). Find the length of the hypotenuse. As \(c^2 = a^2 + b^2\) we have:

sqrt(11^2 + 12^2)

16.278820596099706

Example

A formula from statistics to compute the variance of a binomial random variable with parameters \(p\) and \(n\) is \(\sqrt{n p (1-p)}\). Compute this value for \(p=1/4\) and \(n=10\).

sqrt(10 * 1/4 * (1 - 1/4))

1.3693063937629153

Example

Find the distance between the points \((-3, -4)\) and \((5,6)\). Using the distance formula \(\sqrt{(x_1-x_0)^2+(y_1-y_0)^2}\), we have:

sqrt((5 - -3)^2 + (6 - -4)^2)

12.806248474865697

Example

The formula to compute the resistance of two resistors in parallel is given by: \(1/(1/r_1 + 1/r_2)\). Suppose the resistance is \(10\) in one resistor and \(20\) in the other. What is the resistance in parallel?

1 / (1/10 + 1/20)

6.666666666666666

1.5 Errors

Not all computations on a calculator are valid. For example, the Google calculator will display Error as the output of \(0/0\) or \(\sqrt{-1}\). These are also errors mathematically, though the second is not if the complex numbers are considered.

In Julia, there is a richer set of error types. The value 0/0 will in fact not be an error, but rather a value NaN. This is a special floating point value indicating “not a number” and is the result for various operations. The output of \(\sqrt{-1}\) (computed via sqrt(-1)) will indicate a domain error:

sqrt(-1)

LoadError: DomainError with -1.0:
sqrt was called with a negative real argument but will only return a complex result if called with a complex argument. Try sqrt(Complex(x)).
DomainError with -1.0:
sqrt was called with a negative real argument but will only return a complex result if called with a complex argument. Try sqrt(Complex(x)).

Stacktrace:
 [1] throw_complex_domainerror(f::Symbol, x::Float64)
   @ Base.Math ./math.jl:33
 [2] sqrt
   @ ./math.jl:608 [inlined]
 [3] sqrt(x::Int64)
   @ Base.Math ./math.jl:1531
 [4] top-level scope
   @ In[48]:1

Other calls may result in an overflow error:

factorial(1000)

LoadError: OverflowError: 1000 is too large to look up in the table; consider using `factorial(big(1000))` instead
OverflowError: 1000 is too large to look up in the table; consider using `factorial(big(1000))` instead

Stacktrace:
 [1] factorial_lookup
   @ ./combinatorics.jl:19 [inlined]
 [2] factorial(n::Int64)
   @ Base ./combinatorics.jl:27
 [3] top-level scope
   @ In[49]:1

How Julia handles overflow is a study in tradeoffs. For integer operations that demand high performance, Julia does not check for overflow. So, for example, if we are not careful strange answers can be had. Consider the difference here between these powers of 2:

2^62, 2^63, 2^64

(4611686018427387904, -9223372036854775808, 0)

On a machine with \(64\)-bit integers, the first of these two values is correct, the third is clearly “wrong,” and the second clearly “wrong,” as the answer given is negative.

Wrong is in quotes, as though they are mathematically incorrect, computationally they are correct. The last two are due to overflow. The cost of checking is considered too high, so no error is thrown and the values represent what happens at the machine level.

The user is expected to have a sense that they need to be careful when their values are quite large. But the better recommendation is that the user use floating point numbers, which as easy as typing 2.0^63. Though not always exact, floating point values can represent a much bigger range values and are exact for a reasonably wide range of integer values.

Bit-level details

We can see in the following, using using the smaller 8-bit type, what goes on internally with successive powers of 2: the bit pattern is found by shifting the previous one over to the left, consistent with what happens at the bit level when multiplying by 2:

[bitstring(Int8(2)^i) for i in 1:8]

The last line is similar to what happens to 2^64 which is also 0, as seen. The second to last line requires some understanding of how integers are represented internally. Of the 8 bits, the last 7 represent which powers of 2 (2^6, 2^5, …, 2^1, 2^0) are included. The first 1 represents -2^7. So all zeros, as we see 2^8 is, means 0, but "10000000" means -2^7. The largest positive number would be represented as "01111111" or 2^6 + 2^5 + \cdots + 2^1 + 2^0 = 2^7 - 1. These values can be seen using typemin and typemax:

typemin(Int8), typemax(Int8)

(-128, 127)

For 64-bit, these are:

typemin(Int), typemax(Int)

(-9223372036854775808, 9223372036854775807)

And we see, 2^63 is also just typemin(Int).

Warning

In a turnaround from a classic blues song, we can think of Julia as built for speed, not for comfort. All of these errors above could be worked around so that the end user doesn’t see them. However, this would require slowing things down, either through checking of operations or allowing different types of outputs for similar type of inputs. These are tradeoffs that are not made for performance reasons. For the most part, the tradeoffs don’t get in the way, but learning where to be careful takes some time. Error messages often suggest a proper alternative.

Example

Did Homer Simpson disprove Fermat’s Theorem?

Fermat’s theorem states there are no solutions over the integers to \(a^n + b^n = c^n\) when \(n > 2\). In the photo accompanying the linked article, we see:

\[ 3987^{12} + 4365^{12} - 4472^{12}. \]

If you were to do this on most calculators, the answer would be \(0\). Were this true, it would show that there is at least one solution to \(a^{12} + b^{12} = c^{12}\) over the integers - hence Fermat would be wrong. So is it \(0\)?

Well, let’s try something with Julia to see. Being clever, we check if \((3987^{12} + 4365^{12})^{1/12} = 4472\):

(3987^12 + 4365^12)^(1/12)

28.663217591132355

Not even close. Case closed. But wait? This number to be found must be at least as big as \(3987\) and we got \(28\). Doh! Something can’t be right. Well, maybe integer powers are being an issue. (The largest \(64\)-bit integer is less than \(10^{19}\) and we can see that \((4\cdot 10^3)^{12}\) is bigger than \(10^{36})\). Trying again using floating point values for the base, we see:

(3987.0^12 + 4365.0^12)^(1/12)

4472.000000007058

Ahh, we see something really close to \(4472\), but not exactly. Why do most calculators get this last part wrong? It isn’t that they don’t use floating point, but rather the difference between the two numbers:

(3987.0^12 + 4365.0^12)^(1/12) - 4472

7.057678885757923e-9

is less than \(10^{-8}\) so on a display with \(8\) digits may be rounded to \(0\).

Moral: with Julia and with calculators, we still have to be mindful not to blindly accept an answer.

1.6 Questions

Question

Compute \(22/7\) with Julia.

Question

Compute \(\sqrt{220}\) with Julia.

Question

Compute \(2^8\) with Julia.

Question

Compute the value of

\[ \frac{9 - 5 \cdot (3-4)}{6 - 2}. \]

Question

Compute the following using Julia:

\[ \frac{(.25 - .2)^2}{(1/4)^2 + (1/3)^2} \]

Question

Compute the decimal representation of the following using Julia:

\[ 1 + \frac{1}{2} + \frac{1}{2^2} + \frac{1}{2^3} + \frac{1}{2^4} \]

Question

Compute the following using Julia:

\[ \frac{3 - 2^2}{4 - 2\cdot3} \]

Question

Compute the following using Julia:

\[ (1/2) \cdot 32 \cdot 3^2 + 100 \cdot 3 - 20 \]

Question

You are asked to cook chicken is an unfamiliar kitchen. Your recipe says to turn the oven to 200 Celsius, but you the oven is calibrated in Fahrenheit. Which value is closest?

Select an item

350

375

400

425

450

The recipe says cook until the internal temperature is 165 degrees Fahrenheit. However, the food thermometer in the kitchen is calibrated in Celsius. Which value is closest?

Select an item

68

70

72

74

76

78

80

(Use \(F = 9/5\cdot C + 32\) and \(C = 5/9(F-32)\).)

Question

Which of the following is a valid Julia expression for

\[ \frac{3 - 2}{4 - 1} \]

that uses the least number of parentheses?

Select an item

3 - 2 / (4 - 1)

(3 - 2)/ 4 - 1

(3 - 2) / (4 - 1)

Question

Which of the following is a valid Julia expression for

\[ \frac{3\cdot2}{4} \]

that uses the least number of parentheses?

Select an item

3 * 2 / 4

(3 * 2) / 4

Question

Which of the following is a valid Julia expression for

\[ 2^{4 - 2} \]

that uses the least number of parentheses?

Select an item

2 ^ (4 - 2)

(2 ^ 4) - 2

2 ^ 4 - 2

Question

In the U.S. version of the Office, the opening credits include a calculator calculation. The key sequence shown is 9653 + which produces 11532. What value was added to 9653?

Question

We saw that 1 / 2 / 3 / 4 / 5 / 6 is about \(14\) divided by \(10,000\). But what would be a more familiar expression representing it:

Select an item

1 / 2 * 3 / 4 * 5 / 6

1 /(2 * 3 * 4 * 5 * 6)

1 / (2 / 3 / 4 / 5 / 6)

Question

One of these three expressions will produce a different answer, select that one:

Select an item

(2 - 3) - 4

2 - 3 - 4

2 - (3 - 4)

Question

One of these three expressions will produce a different answer, select that one:

Select an item

2 - 3 * 4

2 - (3 * 4)

(2 - 3) * 4

Question

One of these three expressions will produce a different answer, select that one:

Select an item

-1^2

(-1)^2

-(1^2)

Question

What is the value of \(\sin(\pi/10)\)?

Question

What is the value of \(\sin(52^\circ)\)?

Question

What is the value of

\[ \frac{\sin(\pi/3) - 1/2}{\pi/3 - \pi/6} \]

Question

Is \(\sin^{-1}(\sin(3\pi/2))\) equal to \(3\pi/2\)? (The “arc” functions do no use power notation, but instead a prefix of a.)

Select an item

Yes

No

Question

What is the value of round(3.5000)

Question

What is the value of sqrt(32 - 12)

Question

Which is greater \(e^\pi\) or \(\pi^e\)?

Select an item

\(e^{\pi}\)

\(\pi^{e}\)

Question

What is the value of \(\pi - (x - \sin(x)/\cos(x))\) when \(x=3\)?

Question

Factorials in Julia are computed with the function factorial, not the postfix operator !, as with math notation. What is \(10!\)?

Question

Will -2^2 produce 4 (which is a unary - evaluated before ^) or -4 (which is a unary - evaluated after ^)?

Select an item

-4

4

Question

A twitter post from popular mechanics generated some attention.

Order of operations

What is the answer?

Does this expression return the correct answer using proper order of operations?

8÷2(2+2)

1

Select an item

Yes

No

Why or why not:

Select an item

The precedence of numeric literal coefficients used for implicit multiplication is higher than other binary operators such as multiplication (*), and division (/, \, and //)

Of course it is correct.

Question

Sagan’s number is defined to be the total number of stars in the observable universe. How big is it? A sextillion is 7 groups of three 0’s after a leading 1. One estimate is \(10\) sextillion. How might this be entered into Julia? Select the one that doesn’t work:

With an integer base, 10^21 overflows. For typical integers, only 10^18 is defined as expected. Once 10^19 is entered the mathematical value is larger the the typemax for Int64 and so the value wraps around. The number written out with underscores to separate groups of 0s is parsed as an integer with 128 bits, not 64.

The estimate of 10 sextillion for Sagan’s number was made in 1980, a more modern estimate is 30 times larger.

Question

(From stackoverflow.)

Since 1983, the speed of light is defined to be exactly equal to 299,792,458 meters per second. This can be used to find the value of the Planck length using the formula

\[ l_p = \sqrt{\frac{\hbar\cdot G}{c^3}} \]

Attempting to compute this, we have:

c = 299_792_458;  # the speed of light
G = 6.67430e-11;  # Gravitational constant
h = 6.62607015e-34;  # Planck's constant
h_bar = h / (2*pi);
planck_length = sqrt(h_bar * G / c^3)

3.5793584153084007e-32

That all seems great, but the Wikipedia article says this value is around \(10^{-35}\) not \(10^{-32}\). What is a possible answer?

Yes, this is computed incorrectly. The value c^3 overflows as the actual value is around \(10^{25}\), but the computed value is only around \(10^{18}\). With c defined as above, it will be parsed as an integer, which by default (on most machines) will be stored with \(64\) bits. Operations with 64-bit integers that mathematically produce values bigger than about \(10^{18}\) will be incorrectly computed, as Julia uses a silent means to handle the overflow. (This allows integer computations to be faster.) The suggested approach is to use floating point values to define such values. Floating point can store integer values accurately up to values of \(2^{53}\) (about \(10^{15}\)) and gracefully for larger values, such as \(c^3\) in this problem. With c defined by c = 299792458.0 the computed value for the Planck length is 1.6162550244237053e-35, in agreement with the Wikipedia value.