43 Area between curves

This section uses these add-on packages:

using CalculusWithJulia
using Plots; plotly()
using Roots
using QuadGK
using SymPy

43.1 Area enclosed between two curves

The definite integral gives the “signed” area between the function $f(x)$ and the $x$-axis over $[a,b]$. Conceptually, this is the area between two curves, $f(x)$ and $g(x)=0$. More generally:

Area between two curves

Suppose $f(x)$ and $g(x)$ are integrable functions on $[a,b]$ and $f(x) \geq g(x)$. Then the area between the curves given by $f(x)$ and $g(x)$ over the interval $[a,b]$ is given by: \[ \int_a^b \left(f(x) - g(x)\right) dx \]

In general, this integral yields the “signed” area between the two curves.

Consider Figure 43.1. The shaded rectangle has area: $(f(c)-g(c)) \cdot (x_{i+1}-x_i)$ for some $x_i \le c \le x_{i+1}$. This is suggestive of a term in a Riemann sum of the integral of $f(x) - g(x)$.

Figure 43.1: Illustration of a Riemann sum approximation to estimate the area between $f(x)$ and $g(x)$ over an interval $[a,b]$.

Example

Find the area between $f(x) = \sqrt{x}$ and $g(x) = x^2$ over $[1/4, 3/4]$. As $f(x) \geq g(x)$ on this interval, we have:

\[ \int_{1/4}^{3/4} (x^{1/2} - x^2) dx = (\frac{x^{3/2}}{3/2} - \frac{x^3}{3})\Big|_{1/4}^{3/4} = \frac{\sqrt{3}}{4} -\frac{7}{32}. \]

For the same functions, find the area between the functions over $[1/4, 4]$.

The two graphs cross at $x=1$, so this would need to be done with two integrals:

\[ \begin{align*} A &= \int_{1/4}^{1} (x^{1/2} - x^2) dx + \int_1^4 (x^2 - x^{1/2}) dx\\ &= \left(\frac{x^{3/2}}{3/2} - \frac{x^3}{3}\right) \Big|_{1/4}^1 + \left(\frac{x^3}{3} - \frac{x^{3/2}}{3/2}\right) \Big|_1^4\\ &= \left(\left[\frac{2}{3} - \frac{1}{3}\right]- \left[\frac{1}{12} - \frac{1}{192}\right] + \left[\frac{64}{3} - \frac{16}{3}\right] - \left[\frac{1}{3} - \frac{2}{3}\right]\right)\\ &= \frac{49}{192} \end{align*} \]

Example

Find the area between

\[ \begin{align*} f(x) &= \frac{x^3 \cdot (2-x)}{2} \text{ and } \\ g(x) &= e^{x/3} + (1-\frac{x}{1.7})^6 - 0.6 \end{align*} \]

over the interval $[0.2, 1.7]$. The area is illustrated in Figure 43.1.

f(x) = x^3*(2-x)/2
g(x) = exp(x/3) + (1 - (x/1.7))^6 - 0.6
a, b = 0.2, 1.7
h(x) = g(x) - f(x)
answer, _ = quadgk(h, a, b)
answer

0.6136529762271823

Example

Find the area bounded by the line $y=2x$ and the curve $y=2 - x^2$.

Figure 43.2: Plot of $2-x^2$ and $2x$ over $[-3,3]$ to see the two intersection points.

We plot both curves in Figure 43.2 to see the two intersection points, $a$ and $b$, happen in $[-3, 3]$. These are found numerically through:

f(x) = 2 - x^2
g(x) = 2x
h(x) = f(x) - g(x)
a,b = find_zeros(h, -3, 3)

2-element Vector{Float64}:
 -2.732050807568877
  0.7320508075688773

The answer then can be found numerically:

first(quadgk(h, a, b))

6.928203230275509

Example

Find the integral between $f(x) = \sin(x)$ and $g(x)=\cos(x)$ over $[0,2\pi]$ where $f(x) \geq g(x)$.

Figure 43.3 shows the areas:

Figure 43.3: Plot of $\sin(x)$ and $\cos(x)$ over $[0, 2\pi]$

There is a single interval when $f \geq g$ and this can be found algebraically using basic trigonometry, or numerically:

f(x) = sin(x)
g(x) = cos(x)

a, b = find_zeros(x -> f(x) - g(x), 0, 2pi)  # pi/4, 5pi/4
quadgk(x -> f(x) - g(x), a, b)[1]

2.8284271247461903

Example

Find the area between $x^n$ and $x^{n+1}$ over $[0,1]$ for $n=1,2,\dots$.

On this interval we have $x^n \geq x^{n+1}$, so the integral can be found symbolically through:

@syms x::positive n::positive
ex = integrate(x^n - x^(n+1), (x, 0, 1))
together(ex)

$\frac{1}{\left(n + 1\right) \left(n + 2\right)}$

Based on this answer, what is the value of this sum:

\[ \frac{1}{2\cdot 3} + \frac{1}{3\cdot 4} + \frac{1}{4\cdot 5} + \cdots \]

The answer is $1/2$. This is no surprise. In Figure 43.4) the areas computed carve up the area under the line $y=x^1$ over $[0,1]$

Figure 43.4: Plot of $x^n$ over $[0,1]$ for $n$ in $1$ to $20$.

We can check using the summation function of SymPy which is similar in usage to integrate:

summation(1/((n+1) * (n+2)), (n, 1, oo))

$\frac{1}{2}$

Example

Verify Archimedes’ finding that the area of the parabolic segment is $4/3\text{rds}$ that of the triangle joining $a$, $(a+b)/2$ and $b$. Figure 43.1 clearly shows the bigger parabolic segment area.

Figure 43.5: Area of parabolic segment and triangle

For concreteness, let $f(x) = 2-x^2$ and $[a,b] = [-1, 1/2]$, as in the figure. Then the area of the triangle can be computed through:

f(x) = 2 - x^2
a, b = -1, 1/2
𝐜 = (a + b)/2

sac, sab, scb = secant(f, a, 𝐜), secant(f, a, b), secant(f, 𝐜, b)
f1(x) = min(sac(x), scb(x))
f2(x) = sab(x)

A1 = first(quadgk(x -> f1(x) - f2(x), a, b))

0.421875

As we needed three secant lines, we used the secant function from CalculusWithJulia to create functions representing each. Once that was done, we used the min function to facilitate integrating over the top bounding curve, alternatively, we could break the integral over $[a,c]$ and $[c,b]$, as would be recommended for a symbolic approach.

The area of the parabolic segment is more straightforward.

A2 = first(quadgk(x -> f(x) - f2(x), a, b))

0.5625000000000001

Finally, if Archimedes was right, these values should be equal (up to rounding errors)

A1 * 4/3 ≈ A2

true

Example

Find the area bounded by $y=x^4$ and $y=e^x$ when $x^4 \geq e^x$ and $x > 0$.

Figure 43.6 graphs the two functions and shows clearly the largest zero, for afterwards the exponential dominates the power.

Figure 43.6: Plot of $x^4$ and $e^x$ over $[0, 10]$

There must be another zero, though it is hard to see from the graph over $[0,10]$, as $0^4=0$ and $e^0=1$, so the polynomial must cross below the exponential to the left of $5$. (Otherwise, plotting over $[0,2]$ will clearly reveal the other zero.) We now find these intersection points numerically and then integrate:

h1(x) = x^4
h2(x) = exp(x)
a,b = find_zeros(x -> h1(x) - h2(x), 0, 10)
quadgk(x -> h1(x) - h2(x), a, b)[1]

3980.1173881924947

Examples

The area between $y=\sin(x)$ and $y=m\cdot x$ between $0$ and the first positive intersection depends on $m$ (where $0 \leq m \leq 1$). The extremes are when $m=0$, the area is $2$ and when $m=1$ (the line is tangent at $x=0$), the area is $0$. What is it for other values of $m$? Figure 43.7 show the two functions when $m=1/2$.

Figure 43.7: Plot of $\sin(x)$ and $m\cdot x$ over $[0, \pi]$ when $m=1/2$

For a given $m$, the area is found after computing $b$, the intersection point. We express this as a function of $m$ for later reuse:

intersection_point(m) = maximum(find_zeros(x -> sin(x) - m*x, 0, pi))
a1 = 0
b1 = intersection_point(1/2)
first(quadgk(x -> sin(x) - x/2, a1, b1))

0.4207978950529467

In general, the area then as a function of m is found by substituting intersection_point(m) for b:

area(m) = first(quadgk(x -> sin(x) - m*x, 0, intersection_point(m)))

area (generic function with 1 method)

Figure 43.8 shows the relationship and that the function is monotonically decreasing, as would be guessed.

Figure 43.8: Plot of area over $[0,1]$

While here, let’s also answer the question of which $m$ gives an area of $1$, or one-half the total? This can be done as follows:

find_zero(m -> area(m) - 1, (0, 1))

0.2566498569701879

(Which is a nice combination of using find_zeros, quadgk and find_zero to answer a problem.)

Example

In an early 2023 article appearing in the New York Times a discussion on excess deaths was presented. Figure 43.9 shows two curves from which the number of excess deaths can be computed.

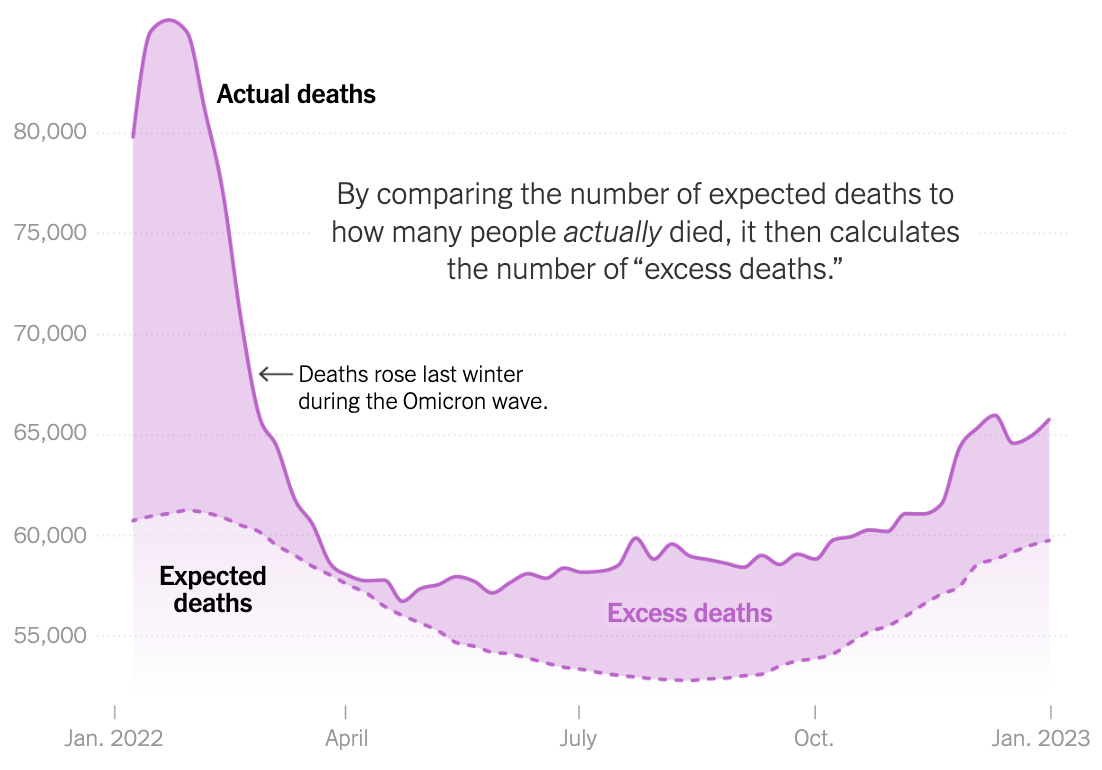
Consider the curve marked Actual deaths. The number of deaths per year is the sum over each day of the number of deaths per each day. Approximating this number with a curve and setting 1 day equal to 1 unit, the number of deaths is basically $\int_0^{365} d(t) dt$. This curve is usually, say, $u(t)$, so the expected number of deaths would be $\int_0^{365} u(t) dt$. The difference, $\int_0^{365} (d(t) - u(t))dt$ is interpreted as the number of excess deaths. This methodology has been used to estimate the true number of deaths attributable to the COVID-19 pandemic.

Example

Consider two overlapping circles, one with smaller radius. How much area is in the larger circle that is not in the smaller?¹

Without losing too-much generality, we can consider the smaller circle to have radius $a$, the larger circle to have radius $b$ and centered at $(0,c)$. We assume some overlap: $a \ge c-b$, but not too much: $c-b \ge 0$ or $0 \le c-b \le a$.

@syms x::real y::real a::positive b::positive c::positive
c₁ = x^2 + y^2 - a^2
c₂ = x^2 + (y-c)^2 - b^2
y₀ = first(solve(c₁ ~ c₂ , y))
x₀ = sqrt(a - y₀^2) # point of intersection

$\sqrt{a - \frac{\left(a^{2} - b^{2} + c^{2}\right)^{2}}{4 c^{2}}}$

Plotting with $a=1, b=3/2, c=2$ we have:

Figure 43.10: Plot of two overlapping circles showing a decomposition that might make finding the area tractable

With this orientation, we can see by symmetry that the area is twice the integral from $[0,x_0]$ and from $[x_0, b]$ provided $0 \le c- b \le a$:

a1 = integrate(c + sqrt(b^2 - x^2) - (sqrt(a^2 - x^2)), (x, 0, x₀))
a2 = integrate(c + sqrt(b^2 - x^2) - (c - sqrt(b^2 - x^2)), (x, x₀, b))
A = 2(a1 + a2)

$- a^{2} \operatorname{asin}{\left(\frac{\sqrt{a - \frac{\left(a^{2} - b^{2} + c^{2}\right)^{2}}{4 c^{2}}}}{a} \right)} - b^{2} \operatorname{asin}{\left(\frac{\sqrt{a - \frac{\left(a^{2} - b^{2} + c^{2}\right)^{2}}{4 c^{2}}}}{b} \right)} + \pi b^{2} + 2 c \sqrt{a - \frac{\left(a^{2} - b^{2} + c^{2}\right)^{2}}{4 c^{2}}} - \sqrt{a - \frac{\left(a^{2} - b^{2} + c^{2}\right)^{2}}{4 c^{2}}} \sqrt{- a + b^{2} + \frac{\left(a^{2} - b^{2} + c^{2}\right)^{2}}{4 c^{2}}} - \sqrt{a - \frac{\left(a^{2} - b^{2} + c^{2}\right)^{2}}{4 c^{2}}} \sqrt{a^{2} - a + \frac{\left(a^{2} - b^{2} + c^{2}\right)^{2}}{4 c^{2}}}$

And for the $a=1, b=3/2, c=2$:

A(a => 1, b => 3//2, c => 2)

$- \frac{9 \operatorname{asin}{\left(\frac{\sqrt{15}}{8} \right)}}{4} - \operatorname{asin}{\left(\frac{3 \sqrt{15}}{16} \right)} + \frac{3 \sqrt{15}}{8} + \frac{9 \pi}{4}$

As a check, when the two circles just touch, or $a = c-b$, we should get the same as the area of a circle with radius $b$ or $b^2 \cdot \pi$:

A(c=>3, a=>1, b=>2)

$4 \pi$

(This could also be done by computing the amount of overlap the two circles have—with a single integral—and subtracting from the area of the larger circle.)

Example

Find the area bounded by the $x$ axis, the line $x-1$ and the function $\log(1 + x)$.

Figure 43.11 shows the basic area.

Figure 43.11: Plot of $\log(1 + x)$, $x-1$, and the $x$ axis over $[0,3]$ used to identify the location of the $x$ value ($b$) of the largest intersection point

The value for “$b$” is found from the intersection point of $\log(x+1)$ and $x-1$, which is near $2$:

j1(x) = log(1 + x)
j2(x) = x - 1
ja = 0
jb = find_zero(x -> j1(x) - j2(x), 2)

2.1461932206205825

We see that the lower part of the area has this condition: if $x < 1$ then use $0$, otherwise use $g(x)$. We can handle this many different ways:

break the integral into two pieces and add:

first(quadgk(x -> j1(x) - zero(x), ja, 1)) + first(quadgk(x -> j1(x) - j2(x), 1, jb))

0.8030726701188743

make a new function for the bottom bound:

j3(x) = x < 1 ? 0.0 : j2(x)
first(quadgk(x -> j1(x) - j3(x), ja, jb))

0.8030726629434394

Turn the picture on its side and integrate in the $y$ variable. To do this, we need to solve for inverse functions:

a1=j1(ja)
b1=j1(jb)
f1(y)=y+1                # y=x-1, so x=y+1
g1(y)=exp(y)-1           # y=log(x+1) so e^y = x + 1, x = e^y - 1
quadgk(y -> f1(y) - g1(y), a1, b1)[1]

0.8030726701188743

Note

When doing problems by hand this latter style can often reduce the complications, but when approaching the task numerically, the first two styles are generally easier, though computationally more expensive.

Integrating in different directions

The last example suggested integrating in the $y$ variable. This could have more explanation.

It has been noted that different symmetries can aid in computing integrals through their interpretation as areas. For example, if $f(x)$ is odd, then $\int_{-b}^b f(x)dx=0$ and if $f(x)$ is even, $\int_{-b}^b f(x) dx = 2\int_0^b f(x) dx$.

Another symmetry of the $x-y$ plane is the reflection through the line $y=x$. This has the effect of taking the graph of $f(x)$ to the graph of $f^{-1}(x)$ and vice versa. Here is an example with $f(x) = x^3$ over $[-1,1]$.

f(x) = x^3
xs = range(-1, stop=1, length=50)
ys = f.(xs)
plot(ys, xs)

Figure 43.12: Plot of inverse function of $x^3$

By switching the order of the xs and ys we “flip” the graph through the line $x=y$.

We can use this symmetry to our advantage. Suppose instead of being given an equation $y=f(x)$, we are given it in “inverse” style: $x = f(y)$, for example suppose we have $x = y^3$. We can plot this as above via:

ys = range(-1, stop=1, length=50)
xs = [y^3 for y in ys]
plot(xs, ys)

Figure 43.13: Plot of function given in inverse style

Suppose we wanted the area in the first quadrant between this graph, the $y$ axis and the line $y=1$. What to do? With the problem “flipped” through the $y=x$ line, this would just be $\int_0^1 x^3dx$. Rather than mentally flipping the picture to integrate, instead we can just integrate in the $y$ variable. That is, the area is $\int_0^1 y^3 dy$. The mental picture for Riemann sums would be have the approximating rectangles laying flat and as a function of $y$, are given a length of $y^3$ and height of “$dy$” (cf. Figure 43.14).

Figure 43.14: The figure suggests that the area under $f(x)$ over $[a,b]$ could be represented as the area between the curves $f^{-1}(y)$ and $x=b$ from $[f(a), f(b)]$

For a less trivial problem, consider the area between $x = y^2$ and $x = 2-y$ in the first quadrant shown in Figure 43.15.

Figure 43.15: Plot of $x=y^2$ and $x = 2-y$

In the figure, the bounded area could be described in the “$x$” variable in terms of two integrals, but in the $y$ variable in terms of the difference of two functions with the limits of integration running from $y=0$ to $y=1$. So, this area may be found as follows:

f(y) = 2-y
g(y) = y^2
a, b = 0, 1
quadgk(y -> f(y) - g(y), a, b)[1]

1.1666666666666667

43.2 The area enclosed in a simple polygon

We now turn our attention to a variation of the area bounded between two curves. A simple polygon is comprised of several non-intersecting line segments, save for the last segment ends where the first begins. These have an orientation, which we take to be counterclockwise. Polygons, as was seen when computing areas related to Archimedes efforts, can be partitioned into simple geometric shapes, for which known areas apply. In this section we discuss partitions that allow the enclosed area to be computed.

43.2.1 The triangle formula

First, let’s work out a formula for the area of a triangle formed by three points: $O=(0,0)$, $P=(x_1, y_1)$, and $Q = (x_2, y_2)$ where we assume the angles for $P$ and $Q$ are as in Figure 43.16 (the angle $0 < \theta < \pi$).

Figure 43.16: Triangle $\triangle OPQ$ with $\theta_2 > \theta_1$

The area of a triangle is $1/2 \cdot b \cdot h$. The base of the triangle in Figure 43.16 is the length of $OP$, the height is the length of $OQ$ times $\sin(\theta)$. We can then compute in terms of coordinates:

\[ \begin{align*} A &= \frac{1}{2} b \cdot h\\ &= \frac{1}{2} \lvert \overline{PQ} \rvert \cdot \lvert\overline{OQ}\rvert \sin(\theta) \\ &= \frac{1}{2} \lvert \overline{PQ} \rvert \cdot \lvert\overline{OQ}\rvert \sin(\theta_2 - \theta_1) \\ &= \frac{1}{2} \lvert \overline{PQ} \rvert \cdot \lvert\overline{OQ}\rvert \left(\sin(\theta_2)\cos(\theta_1) - \cos(\theta_2)\sin(\theta_1)\right) \\ &= \frac{1}{2} \lvert\overline{PQ}\rvert \cdot \lvert\overline{OQ}\rvert \left(\frac{y_2}{\lvert\overline{OQ}\rvert}\frac{x_1}{\lvert\overline{PQ}\rvert} - \frac{x_2}{\lvert\overline{OQ}\rvert}\frac{y_1}{\lvert\overline{PQ}\rvert}\right)\\ &= \frac{1}{2} \left(x_1 y_2 - y_1 x_2 \right). \end{align*} \]

The expression $x_1 y_2 - y_1 x_2$ is sometimes written using determinant notation

\[ x_1 y_2 - y_1 x_2 = \left| \begin{align*} x_1 &\quad x_2\\ y_1 &\quad y_2\\ \end{align*} \right|. \]

Now consider a simple, convex polygon with $(0,0)$ in its interior. We can create triangles to partition the polygon as in Figure 43.17.

Figure 43.17: Partition of simple example using triangles to compute the area inside a simple polygon

The triangles do not overlap, so the area inside the polygon is the sum of the areas of each triangle. This is found from:

\[ \frac{1}{2} \cdot \left( (x_1 y_2 - y_1 x_2) + (x_2 y_3 - y_2 x_3) + (x_3 y_4 - y_3 x_4) + (x_4 y_1 - y_4 x_1) \right) \]

For the points in Figure 43.17 this value is:

xs = [-1,  1,  2,    0, -1]
ys = [-1, -1,  1/2,  1, -1]

(1/2) * sum(xs[i]*ys[i+1] - xs[i+1]*ys[i] for i in 1:4)

3.75

More generally, we have:

Area of a simple polygon described by Cartesian coordinates

The area enclosed in a simple polygon with $n$ points (labeled by $P_i = (x_i, y_i)$) traversed in a counter-clockwise manner is given by:

\[ A = \sum_{i=1}^{n-1} \left(x_i y_{i+1} - y_i x_{i+1}\right) + \left( x_n y_1 - y_n x_1\right). \]

This formula is motivated above by a convex polygon with the origin in its interior, but extends to any simple polygon. This formula is often called Gauss’s shoelace formula, so called as diagrams like Figure 43.18, which are used to help remember what gets multiplied and what terms are subtracted, resemble the laces of shoes.

Figure 43.18: Representation to remember Gauss’s shoelace formula for computing the area of a simple polygon

The above formula computes the area for simple polygon described by Cartesian coordinates and traversed in a counter-clockwise manner. Traversing in a clockwise manner will produce the same number multiplied by $-1$. This formula extends to compute the area of any simple polygon traversed in a counter-clockwise manner. For non-simple polygons, the formula can be applied with care to account for “negative” area when the traversal is in the clockwise manner.

43.2.2 The trapezoid formula

In this example, we see how trapezoids can be used to find the interior area encolosed by a simple polygon, avoiding integration.

Consider a trapezoid formed by points $P_1 = (x_1, y_1)$, $P_2 = (x_2, y_2)$, $P_3 = (x_2, 0)$, and $P_4 = (x_1, 0)$. Assume $x_1 > x_2$. The area is the average of the heights times the length of the base:

\[ A = \frac{1}{2}\left(y_2 + y_1\right) \cdot (x_1 - x_2) = - \frac{1}{2}\left(y_2 + y_1\right) \cdot (x_2 - x_1). \]

Area inside a simple polygon

Consider a simple polygon described by points $(x_1,y_1), (x_2,y_2), \dots, (x_n, y_n)$ Set $(x_{n+1}, y_{n+1}) = (x_1,y_1)$. Assume the points traverse the simple polygon in a counter-clockwise manner. Then the area contained within the polygon is given by the formula:

\[ A = \sum_{i=1}^n \frac{1}{2} \left(y_{i+1} + y_i\right) \cdot \left(x_{i+1} - x_i \right). \]

Each term describes the signed area of a trapezoid, with a sign of $1$ if $x_{i+1} \le x_i$ and $-1$ otherwise.

We illustrate the formula with a simple polygon shown in Figure 43.19. (The same shape as before, but shifted up and over by $2$ units.)

xs = [1, 3, 4,   2, 1] # n = 4 to give 5=n+1 values
ys = [1, 1, 5/2, 3, 1]
plt = plot(; line=(3, :black), framestyle=:origin, aspect_ratio=:equal, legend=false)

plot!(plt, xs, ys)
scatter!(plt, xs,  ys; marker=(5, :black))

Figure 43.19: A simple polygon whose area can be computed by the trapezoid formula

Going further, we draw the four trapezoids associated to Figure 43.19 using different colors (blue or yellow) depending on the sign of the xs[i+1] - xs[i] terms in Figure 43.20.

Figure 43.20: Simple polygon of Figure 43.19 with trapezoids used to compute area filled in

The yellow trapezoids appear to be colored grey, as they completely overlap with parts of the blue trapezoids and blue and yellow display as grey. As the signs of the differences of the $x$ values are different, these areas add to $0$ in the sum, leaving just the area of the interior when the sum is computed.

For this particular figure, the enclosed area is

- sum((ys[i+1] + ys[i]) / 2 * (xs[i+1] - xs[i]) for i in 1:length(xs)-1)

3.75

43.2.3 Area between a parameterized curve

Now suppose a closed, simple curve is parameterized in the counterclockwise direction by $(f(t), g(t))$ for $t$ in $[a,b]$. The area contained in the curve is approximated by the area contained in the polygon given by the points $(f(t_i), g(t_i))$ where $a = t_0 < t_1 < \cdots < t_n = b$ is some partition. The approximate area is given by:

\[ \begin{align*} A &= - \sum_{i=1}^n \frac{y_{i+1} + y_i}{2} \cdot (x_{i+1} - x_i)\\ &= -\frac{1}{2} \sum_{i=1}^n \left(g(t_{i+1}) + g(t_i)\right)\cdot\left(f(t_{i+1}) - f(t_i)\right)\\ &= -\frac{1}{2} \sum_{i=1}^n \left(g(t_{i+1}) + g(t_i)\right)\frac{f(t_{i+1}) - f(t_i)}{t_{i+1} - t_i}\left(t_{i+1} - t_i\right)\\ &\approx -\frac{1}{2} \int_a^b 2g(t) f'(t) dt\\ &= -\int_a^b g(t) f'(t) dt \\ &= \int_a^b f(t) g'(t) dt. \end{align*} \]

The last line follows by integration by parts.

Area of bounded by a parameterized curve

Let $(f(t), g(t))$, $a \le t \leg b$ parameterize a closed, simple curve. Then the area bounded by the curve is given by:

\[ A = \sigma \cdot \int_a^b f(t) g'(t) dt, \]

where $\sigma = 1$ if the parameterization is in the counter-clockwise direction, and $\sigma = -1$ if the parameterization is in the clockwise direction.

Example

The area of a circle is well known, $\pi r^2$. Here we compute it with the above formula using the following parameterization of the perimeter:

@syms t, R
u = R * cos(t)
v = R * sin(t)
integrate(u * diff(v,t), (t, 0, 2PI))

$\pi R^{2}$

Example

Talbot’s curve is parametrically described by

\[ \begin{align*} u(t) &= \frac{1}{a} \cdot (a^2 + c^2 \cdot \sin(t)^2) \cdot \cos(t)\\ v(t) &= \frac{1}{b} \cdot (a^2 - 2c^2 + c^2 \cdot \sin(t)^2)\cdot \sin(t) \end{align*} \]

Find the area bounded by the curve when $a=2$, $b=1$, and $c=3$.

Figure 43.21 shows the curve with the given set of constants.

Figure 43.21: Talbot’s curve with $a=2$, $b=1$, and $c=3$

We can integrate in terms of the parameters. However, this parameterization is in the clockwise direction, so we reverse our limits of integration below:

@syms a b c t
u = (a^2 + c^2*sin(t)^2)*cos(t)/a
v = (a^2 - 2c^2 + c^2*sin(t)^2)*sin(t)/b
A = integrate(u * diff(v, t), (t, 2PI, 0)) # reverse limits to adjust for parameterization

$- \frac{\frac{\pi a^{4}}{b} - \frac{\pi a^{2} c^{2}}{b} - \frac{\pi c^{4}}{8 b}}{a}$

Finally, we substitute in the specific parameter values:

A(a=>2, b=>1, c=>3)

$\frac{241 \pi}{16}$

43.3 Questions

Question

Find the area enclosed by the curves $y=2-x^2$ and $y=x^2 - 3$.

Question

Find the area between $f(x) = \cos(x)$, $g(x) = x$ and the $y$ axis.

Question

Find the area between the line $y=1/2(x+1)$ and half circle $y=\sqrt{1 - x^2}$.

Question

Find the area in the first quadrant between the lines $y=x$, $y=1$, and the curve $y=x^2 / 4$.

Question

Find the area between $y=x^2$ and $y=-x^4$ for $\lvert x \rvert \leq 1$.

Question

Let f(x) = 1/(sqrt(pi)*gamma(1/2)) * (1 + x^2)^(-1) and g(x) = 1/sqrt(2*pi) * exp(-x^2/2). These graphs intersect in two points. Find the area bounded by them.

(Where gamma(1/2) is a call to the gamma function.)

Question

Find the area in the first quadrant bounded by the graph of $x = (y-1)^2$, $x=3-y$ and $x=2\sqrt{y}$. (Hint: integrate in the $y$ variable.)

Question

Find the total area bounded by the lines $x=0$, $x=2$ and the curves $y=x^2$ and $y=x$. This would be $\int_a^b \lvert f(x) - g(x) \rvert dx$.

Question

Look at the sculpture Le Tamanoir by Calder. A large scale work. How much does it weigh? Approximately?

Let’s try to answer that with an educated guess. The right most figure looks to be about 1/5th the total amount. So if we estimate that piece and multiply by 5 we get a good guess. That part looks like an area of metal bounded by two quadratic polynomials. If we compute that area in square inches, then multiply by an assumed thickness of one inch, we have the cubic volume. The density of galvanized steel is 7850 kg/$m^3$ which we convert into pounds/in$^3$ via:

7850 * 2.2 * (1/39.3)^3

0.28452123585283234

The two parabolas, after rotating, might look like the following (with $x$ in inches):

\[ f(x) = x^2/70, \quad g(x) = 35 + x^2/140 \]

Put this altogether to give an estimated weight in pounds.

Is the guess that the entire sculpture is more than two tons?

Note

We used area to estimate weight in this example, but Galileo used weight to estimate area. It is mentioned by Martin that in order to estimate the area enclosed by one arch of a cycloid, Galileo cut the arch from some material and compared the weight to the weight of the generating circle. He concluded the area is close to $3$ times that of the circle, a conjecture proved by Roberval in 1634.

Question

Formulas from the business world say that revenue is the integral of marginal revenue or the additional money from selling 1 more unit. (This is basically the derivative of profit). Cost is the integral of marginal cost, or the cost to produce 1 more. Suppose we have

\[ \text{mr}(x) = 2 + \frac{e^{-x/10}}{1 + e^{-x/10}}, \quad \text{mc}(x) = 1 + \frac{1}{2} \cdot \frac{e^{-x/5}}{1 + e^{-x/5}}. \]

Find the profit to produce 100 units: $P = \int_0^{100} (\text{mr}(x) - \text{mc}(x)) dx$.

Question

Can SymPy do what Archimedes did?

Consider the following code which sets up the area of an inscribed triangle, A1, and the area of a parabolic segment, A2 for a general parabola:

@syms x::real A::real B::real C::real a::real b::real
c = (a + b) / 2
f(x) = A*x^2 + B*x + C
Sec(f, a, b) = f(a) + (f(b)-f(a))/(b-a) * (x - a)
A1 = integrate(Sec(f, a, c) - Sec(f,a,b), (x,a,c)) + integrate(Sec(f,c,b) - Sec(f,a,b), (x, c, b))
A2 = integrate(f(x) - Sec(f,a,b), (x, a, b))
out = 4//3 * A1 - A2

$\frac{A a^{3}}{3} + A a^{2} b - A a b^{2} - \frac{A b^{3}}{3} + a^{2} \left(- \frac{A a}{2} - \frac{A b}{2}\right) - \frac{4 a^{2} \left(\frac{A a}{4} - \frac{A b}{4}\right)}{3} - \frac{4 a \left(- \frac{A a^{2}}{2} + \frac{A a b}{2}\right)}{3} - b^{2} \left(- \frac{A a}{2} - \frac{A b}{2}\right) + \frac{4 b^{2} \left(- \frac{A a}{4} + \frac{A b}{4}\right)}{3} + \frac{4 b \left(\frac{A a b}{2} - \frac{A b^{2}}{2}\right)}{3} - \frac{4 \left(\frac{a}{2} + \frac{b}{2}\right)^{2} \left(- \frac{A a}{4} + \frac{A b}{4}\right)}{3} + \frac{4 \left(\frac{a}{2} + \frac{b}{2}\right)^{2} \left(\frac{A a}{4} - \frac{A b}{4}\right)}{3} + \frac{4 \left(\frac{a}{2} + \frac{b}{2}\right) \left(- \frac{A a^{2}}{2} + \frac{A a b}{2}\right)}{3} - \frac{4 \left(\frac{a}{2} + \frac{b}{2}\right) \left(\frac{A a b}{2} - \frac{A b^{2}}{2}\right)}{3}$

Does SymPy get the correct output, $0$, after calling simplify?

Question

In Martin a fascinating history of the cycloid can be read.

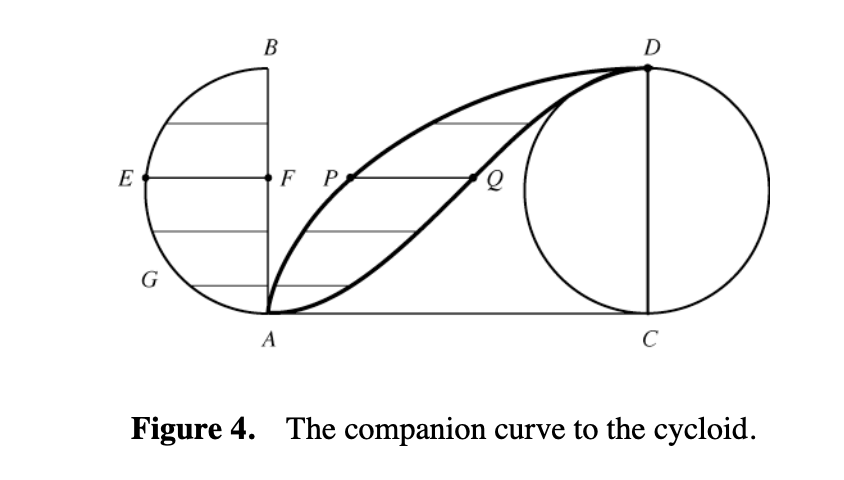
Figure 43.22: Figure from Martin showing the companion curve to the cycloid. As the generating circle rolls, from `A` to `C`, the original point of contact, `D`, traces out an arch of the cycloid. The companion curve is that found by congruent line segments. In the figure, when `D` was at point `P` the line segment `PQ` is congruent to `EF` (on the original position of the generating circle).

In particular, it can be read that Roberval proved that the area between the cycloid and its companion curve is half the area of the generating circle. Roberval didn’t know integration, so finding the area between two curves required other tricks. One is called “Cavalieri’s principle.” From the figure above, which of the following would you guess this principle to be:

Suppose the generating circle has radius $1$, so the area shown is $\pi/2$. The companion curve is then $1-\cos(\theta)$ (a fact not used by Roberval). The area under this curve is then

@syms theta
integrate(1 - cos(theta), (theta, 0, SymPy.PI))

$\pi$

That means the area under one-half arch of the cycloid is

Doubling the answer above gives a value that Galileo had struggled with for many years.

Roberval, avoiding a trignoometric integral, instead used symmetry to show that the area under the companion curve was half the area of the rectangle, which in this figure is $2\pi$.

Question

Figure 43.23: Cavalieri example

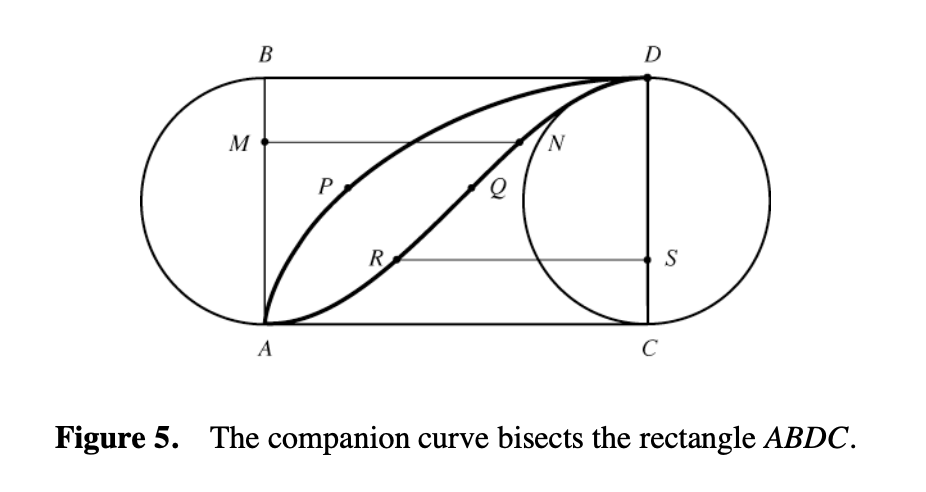
Figure 43.23 shows on same scale the graphs of $f(x)$ and $g(x)$ and the graphs of $f(x) - g(x)$ and $0$ (the lower figure). Twenty lines were drawn with height $f(x) - g(x)$ on the lower figure and these were translated to the upper figure by an amount $g(x)$. All to illustrate that any parallel line in the $y$ direction intersects the two figures with the same length.

What does this imply:

Question

Consider the polygon defined by the points $P_1 = (0,0), P_2 = (1, 1/2), P_3 = (2,2)$, and $P_4=(1,3)$. What is the enclosed area?

Question

Consider the Polygon defined by the points $P_1 =(0,0), P_2 = (2, 0), P_3 = (0,1), P_4=(2,2)$, and $P_5=(0,2)$. What is the enclosed area?

Now move $P_3$ to $(4,1)$. Will the enclosed area by $4$ units more?

Question

A folium can be parameterized by $(f(t), g(t)) = (r(t)(t), r(t) (t)), where $r(t) = -\cos(t) + 4 \cdot \cos(t) \cdot \sin^2(t)$.

Compute the area between $a=$`0.5236$ and $b=\pi/2$ (cf. Figure 43.24).

Figure 43.24: Plot of a folium—a parameterized curve—over $[0, 2\pi]$ with interval $[$`0.5236`$,\pi/2]$ emphasized

This question came up on the Julia discourse discussion board. A solution, modified from an answer of @rocco_sprmnt21 is followed.↩︎